Principles of Quantitative Image Analysis

Quantitative Image Analysis, Part 1 Principles

Early lnvestigations
P.P. Anosov first used the metallurgical microscope in 1841 to reveal the structure of a Damascus knife [1]. Driven by natural curiosity, the very next question proposed was probably "what are the volume fractions of constituents?" The first quantitative stereological relationship developed for microscopy is attributed to A. Delesse [2] in 1848. From his work, the relationship A_A = V_V (i.e., the area fraction equals the volume fraction) was derived. Many of the early studies of metallography are attributed to Sorby. He traced the images of rock onto paper by using projected light. After cutting out the different phases present and weighing the pieces from each phase, the volume fraction of the phases was determined. The relationship between lineal analysis and volume fractions, L_L= V_V (i.e., the lineal fraction equals the volume fraction) was demonstrated by Rosiwal in 1898 [3]. One of the first studies to correlate chemical compositions with structure was made by Albert Sauveur in 1896 [4]. From this work, the relationship between the carbon content of plain-carbon steel and the volume fraction of the various constituents was discovered. The relationship between volume fraction and points in a test grid was established both by Thompson [5] and Glagolev [6] in 1930 and 1931, respectively (as well as by several other subsequent workers in other disciplines). Thus, the relationship P_P = V_V (i.e., the point fraction equals the volume fraction) came into existence. From these first experimenters, that almost spanned a century, the now well known relationship P_P = L_L= A_A = V_V has evolved.

Point Counting
Of all these manual procedures, point counting is probably the most important. From a metallographers perspective, it is the easiest way to manually estimate the volume fraction of a specific constituent. Regarding image analysis, point counting will be shown to be equally important. In reality an image analysis system is only a simple point counter. However, when working in conjunction with an electronic computer, highly sophisticated analysis algorithms can be performed rapidly. It would, of course, be possible to perform the same measurements by manual methods, but the time to perform these measurements would be astronomical!

Video Microscopy
The best remembered commercial demonstration of television was made by NBC at the 1939 New York World's Fair. However, television as we know it today, has evolved from the early work of Philo Taylor Farnsworth in the 1920's, and several commercial demonstrations in the late 1920's and early 30's [7]. Commercialization of this technology did not occur until after World War I because of the need to produce radar systems for the military. One early video technique used the 'flying Spot'. The output of a cathode ray tube was used as the source of illumination. This bright spot was rastered across the specimen and a detector tube was used to analyze the output signal. Systems such as this were used to evaluate blood cells [8] and to assess nonmetallic inclusions in steels [9]. As the technology advanced, ordinary television cameras were used to convert the output signal of the microscope into an electronic signal and a corresponding image on a video tube. These early systems were analog devices.

Image Analysis Systems
Concurrent with advances in video systems, analog and later digital computers were being developed. In 1963, the first analysis system to use a television camera as the input device was developed. This system was made by Metals Research Ltd., Cambridge, England, and was called the Quantimet A [10]. The term 'QTM' has been applied to image analysis systems because the Quantimet A was referred to as a Quantitative Television Microscope. While this system did little more than serve as a densitometer, it was the beginning of the age of automation. The successor to this system was the Quantimet B. This was the first commercially successful system. It was capable of making simple stereological measurements of an entire field of view as well as offering a digital readout of the gray level. Through time, Metals Research has become IMANCO, Cambridge Instruments and, more recently, Leica. The first system capable of storing a full black and white image was the Bausch and Lomb QMS [11]. This system was introduced in 1968. In conjunction with a light pen, measurements of properties of individual objects (now referred to as feature specific analysis), were possible for the first time. A fully digital I/A system, the Quantimet 720, was introduced by IMANCO in 1969.

Major advances in texture analysis and mathematical morphological analysis were being developed at Ecole de Mines in Paris, France [12]. This group was responsible for developing image erosion, dilation, skeletonization and other concepts, plus the use of Boolean binary logic. The first I/A system to utilize these functions was the Leitz TAS (Texture Analysis System) introduced in 1974. Buehler's original image analyzer, the OMNlMET was introduced in 1978. As computer systems became faster, software based I/A systems were introduced by Joyce-Loebl, KONTRON and Cambridge Instruments. Complete images could be stored in the computer memory of these systems; thus, gray and binary image processing was possible. The widespread use of the personal computer led to further advances in I/A technology in the early 1980's.

Today's fourth generation I/A systems represent a new marriage of hardware and software. Special processing boards that fit in standard microcomputers are used to perform functions such as gray level transformations and numerous binary operations. These boards are composed of numerous modules, and software modules are used for control of the hardware modules. The software libraries use programming languages such as Basic or C. The manufacturers of image analysis systems create user interfaces so that relatively simple instructions can be used to interface with the software libraries and thus control the image processing functions [13]. The net result is that the high speed of the hardware boards, in combination with relatively user- friendly interface systems, allow complex image analysis operations to be performed with simple instructions.

Gray lmages
The accuracy and repeatability of measurements made by I/A systems are dependent upon numerous variables. The quality and integrity of the specimens that are to be evaluated are probably the most critical factors in image analysis. No I/A system can compensate for poorly prepared specimens. To obtain meaningful results, the best possible procedures for polishing and etching the specimens to be observed must be employed. Factors such as inclusion pull- out, comet tails, poor or variable contrast caused by improper etching can not be eliminated by the I/A system. One of the most common hardware variables that can effect the system's performance is the light optical microscope's illumination system. Proper alignment of the microscope lamp and correct adjustment are of paramount importance for optimum performance of the I/A system.

One of the most common hardware variables that can effect the system's performance is the light optical microscope's illumination system. Proper alignment of the microscope lamp and correct adjustment are of paramount importance for optimum performance of the I/A system. The alignment, resolution and response of the TV scanner used to convert the optical image into an electrical signal has a large influence upon the performance of the I/A system. After properly aligning the microscope, some minor variations in the gray level of a blank image may be noted. Because neither the scanner tube nor the lenses in the microscope are perfect, some slight variations in the gray image can occur. The shading corrector observes each pixel in a blank image and adjusts their gray levels to produce a uniform white background. This correction factor is then applied to every image to correct for minor problems in the system. If a large degree of correction is required, this may indicate that the microscope is grossly misaligned, or the scanner tube has deteriorated from use. Once these concerns have been properly rationalized, the next major variable to consider is how to select the gray level of the objects to be characterized.

To understand how to properly select the gray level of the features to be measured, the manner by which the TV scanner converts the optical image into an electrical signal must be considered. The monitor image is composed of many scanned lines. Relative to the monitor, the TV camera scans the image from left to right and from the top to the bottom of the screen. The image is actually composed of a large number of small square elements called pixels. For an image of a normal microstructure, the gray levels of the pixels on the monitor will range from dark to bright. Historically, black has been assigned a gray level of zero, and white has been assigned the highest value of possible gray levels. Older systems used 6 bits of gray, so white had a gray level of 2⁶ - 1 = 63; today, most I/A systems use 8 bits of gray, so white is 2⁸ - 1 = 255. A schematic of a portion of a monitor is illustrated in Figure 1.

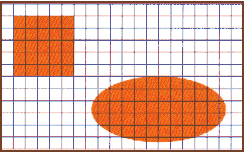	In this drawing, each small square is a pixel. For this example, the square and the ellipse are assumed to have a uniform gray level, lets say 125, and the gray level of the background is white, 255. As an ideal beam scans across the upper portion of Figure 1, the background pixels are counted as gray levels of 255.
Figure 1. Uniform gray level square and ellipse.

When the beam enters the square, a gray level value of 125 is recorded for each pixel contained within the square. Thus, the gray level histogram for this portion of the image would contain 25 squares of gray level 125, and the remaining pixels would all have a gray level of 255, Figure 2a. A cumulative gray level distribution for this case would appear as in Figure 2b.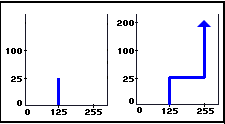

Figures 2a and 2b (left to right) Gray level histogram and cumulative gray level distribution for the ideal square.

Now consider the ideal ellipse. By definition, the gray level of the ellipse is 125; however, notice how the I/A system "sees" the ellipse, or more specifically, consider a pixel on the perimeter of the ellipse. No pixel on the perimeter of the ellipse completely contains all white or all gray. Thus, the pixels on the perimeter of the ellipse contain gray material that is white, 255, and gray material that is the level of the ellipse, 125.

Thus, these pixels have a gray level that can vary between 125 and 255. The histogram and cumulative distributions for the ellipse would appear as illustrated in Figures 3a and b, respectively. What would happen to the square if it were slightly shifted or rotated from the position shown in Figure 1? In reality, a square having this orientation would occur very rarely. Any object viewed in an I/A system will be, at best, the ideal ellipse.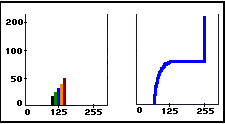

Figures 3a and 3b (left to right) Ellipse histogram and cumulative gray level histogram.

These examples illustrate some of the problems that can be encountered with an ideal scanner. There are several other problems that should be considered. In the previous examples, as the rastered beam moves from a bright area to a dark area, there may be some under detection occurring. Conversely, as the beam moves from the dark area to a bright area, some over shoot may occur. This phenomena can even occur for objects with very sharp edges and uniform gray levels such as an e-beam machined circle, Figure 4.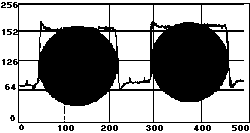

Figure 4. Scanner response for E-Beam machined circles.

For etched specimens that usually do not have extremely sharp edges, there is a transition zone between the matrix and the etched constituent. Thus, in the direction of scanning, determining the true edge or boundary of the object to be measured may not be a straightforward problem.

Sharpening of the edges of features can be handled several ways by image analysis systems. A filter such as the 3 x 3 matrix composed of elements a,b,c,...,i can be used. Consider an image that has a boundary that contains a light gray region surrounding a much darker object. In particular, consider the pixel whose gray level is 120, the center pixel in the 3 x 3 matrix shown below. Applying a filter of the form:

to

yields the new pixel value of:

new = a*240 + b*110 + c*19
          +d*255 + e*120 + f*20
          +g*270 + h*130 + i*21

The matrix containing elements a,b,...,i is called a Kernel. Several common filters and the corresponding Kernels are contained in Table 1.

Table 1. Gray Processing Functions Operator Kernel Comments Low Pass Mean *(1/9) Smoothing Median Smoothing, e is replaced by the median value pixel of a, b, ..i Gaussian Smoothing Laplacian Edge Enhancement Gradient Edge Enhancement Smooth *(1/4) Noise Reduction

Many other types of gray imaging processing are possible [14]. These examples serve to illustrate some of the more common operators and how they can be applied. In older I/A systems, these types of gray image processing were very slow. However, this type of image processing is done at very high rates with Pentium processor based computer systems.

The transition from one zone to another can be resolved by hardware. This is referred to as autodelination. The autodelinator automatically selects the point at which the change in video signal is 50% and then squares off the output signal.

Image Measurements
Consider only the square composed of pixels having a gray level of 125, Figure 1. For this image, if all the pixels having a gray level of less than 200 were counted, only the pixels within the square would be used for measurements. A binary image of this field of view can be formed by letting the detected pixels be white and the remaining pixels be black. In this example, assume that each pixel is 2mm long and 2mm high. Thus, the perimeter of the square is 5 + 5 + 5 + 5 pixels and, since the pixels are 2mm long, the actual perimeter of the square is (20 pixels) * 2mm/pixel = 40mm. Similarly, the area of the square is 25 pixels², and the actual area is 25 pixels²* 4mm²/pixel =100mm².

Images to be analyzed usually contain many objects or regions of interest to be measured. The way objects are selected and classified for measurement varies somewhat from system to system; however, there are two types of measurements that are common to all I/A systems. These are field measurements and feature measurements. The schematic representation of a monitor has several frames on the screen, Figure 5. The outermost frame is referred to as the video frame. This frame contains every pixel that the TV scanner contains. The frame inside the video frame is referred to as the image frame. Since no measurements are made within the region of the image frame and the video frame, this region is blank. The inner most frame is the live frame or the measuring frame. The objects shown on the monitor schematic are contained within various frames. Objects or portions of objects contained inside the live frame are (red). The portion of objects contained in the region between the live frame and the image frame are (pink). Field measurements are made on every part of objects "a-h" that are within the live frame. For the particular system used by the author, for feature-specific measurements to be made of an object, the lowest point of the feature must be in the live frame. This low point is called the Feature Coincident Point (FCP). Only objects "a", "c", "e", "f" and "g" will be used for feature specific measurements. Since "g" is totally contained within the live frame, all of it will be measured. Object "a" will not be correctly measured because it continues beyond the image frame. Thus, the selection of the magnification to use and the relative sizes of the image frame and the live frame are very important. Other systems operate somewhat differently. Thus, it is important to understand which features are measured and which features are not measured for the particular system being used. Improper selection of the frame positions or magnification can lead to under estimation of the size of larger objects in a microstructure.

Figure 5. Schematic of frames on the monitor image region.

The simplest measurements to make are the primary field measurements, Table 2.

Table 2: Primary Field Measurements Area Total number of detected pixels in the Live Frame times the area of a pixel. Perimeter Total perimeter of detected pixels. Vertical Projection Total length of the detected vertical chords. Horizontal Projection Total length of detected horizontal chords.

Other measurements can be derived from these primary parameters; i.e.,

Area Fraction = Field Area/Live frame area,
Mean chord length = Field Area/Horizontal Projection and
Anisotropy = V. Projection/H. Projection

Often, information regarding each specific feature in the microstructure is required. These measurements are referred to as feature-specific parameters; some of the primary feature-specific measurements include: area, perimeter, horizontal projection, vertical projection, Feret diameter, length and breadth, Table 3 and Figure 6.

Table 3: Selected Feature-Specific Parameters Area Total number of detected pixels in the feature times the area of a pixel. Perimeter Total length of detected pixels on the boundary of the feature. Feret 0 Maximum feature diameter in the direction of the X axis ( 0° ). Feret 90 Maximum feature diameter in the direction of the Y axis ( 90° ). Length Maximum of all the user selected Feret diameters. Breadth Dimension perpendicular to length. X max. Maximum distance along the X axis where detected pixels for the feature are found. X min. Minimum distance along the X axis where detected pixels for the feature are found

Figures 6A and 6B: Examples of feature-specific measurements. Figure 6A Figure 6B

In addition, numerous parameters can be derived from the basic parameters. Some examples include:

Anisotropy = Length/breadth
Roundness = (P²)/(4 pA); and,
Shape Factor = 4 pA/P².

Summary
The principles governing operation of image analysis systems have been described in this Tech-Note. In the 35 years since the Quantimet A was introduced, image analyzers have grown and evolved into very powerful, very useful tools for the microstructural analyst. Proper specimen preparation still emains the key factor governing optimal usage of image analysis systems. Once the correct image contrast has been achieved so that the desired microstructural feature can be observed without interference, it is a relatively simple matter to perform measurements. 

References
1. Anosov, P.P., "Collected Works," Akademiya Nauk,SSSR, 1954.
2. Delesse, A. "Procede mechanique pour determiner la composition des roches," Ann. Mines (IV), 13:379, 1848.
3. Rosiwal, A., "On Geometric Rock Analysis. A Simple Surface Measurement to Determine the Quantitative Content of the Mineral Constituents of a Stony Aggregate." Verhandl. K.K. Geol. Reich., 1898, p.143.
4. Sauveur, A., "The Microstructure of Steel and the Current Theories of Hardening," Trans. AIME, 1896, p. 863.
5. Thompson, E., "Quantitative Microscopic Analysis, J. Geol., 27, 1930, p. 276.
6. Glagolev, A. A., Mineralogical Materials, 1931, p. 10.
7. Fisher, D. E. and Marshall, J. F., "Tube: the Invention of Television," Counterpoint, 1996.
8. Tolles, W. E., "Methods of Automatic Quantification of Micro-Autoradiographs," Lab. Invest., 8, 1959, p. 1889.
9. Bloom, R. A., Walz, H. and Koenig, J. G., "An Electronic Scanner-Computer for Determining the Non-Metallic Inclusion Content of Steels," JISI, 1964, p.107.
10. Leica Imaging Systems History.
11. B&L, 1969.
12. Serra, J., Image Analysis and Mathematical Morphology, Academic Press, 1982.
13. Exner, H. E. and Hougardy, H. P., Quantitative Image Analysis of Microstructures, DGM Informationsgesellschaft mbH, Oberursel, 1988, p. 99-126.