The following article was written by George F. Vander Voort and Gabriel Lucas of Buehler Ltd. It originally appeared in the September, 1998 edition of  Advanced Materials and Processes magazine and is reproduced here with the kind permission of Margaret Hunt, AM&P Editor.

Microindentation
Hardness Testing

Microindentation hardness testing is a very valuable tool for the materials engineer, but it must be used with care and full understanding of potential problems.

The purpose of microindentation hardness testing is to study fine scale changes in hardness, either intentional or accidental. The technique is also commonly known as microhardness testing, but this term is misleading because it implies that the hardness is extremely low, which is not the case. The applied load and the resulting indent size are small relative to bulk tests, but the same hardness number is derived. Consequently, ASTM Committee E-4 on Metallography recommends the term "microindentation hardness testing," which could be given the acronym MHT.

This article describes the two most common microindentation tests -- the Vickers and the Knoop tests, which are currently being updated as ASTM Standard E 384.

The Vickers test In 1925, Smith and Sandland of the United Kingdom developed a new indentation test for metals that were too hard to evaluate by the Brinell test, whose hardened steel ball was limited to steels with hardnesses below ~ 450 HBS (~ 48 HRC). In designing the new indenter, a square-based diamond pyramid (Fig. 1), they chose a geometry that would produce hardness numbers nearly identical to Brinell numbers within the range of both tests. This was a very wise decision, because it made the Vickers hardness test very easy to adopt.

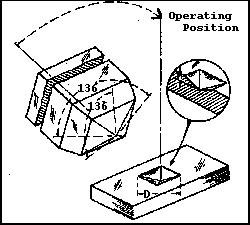Fig. 1- Schematic diagram showing the shape of the Vickers indenter and impression. The Vickers hardness number is calculated based on the surface area of the indent.

The ideal d / D ratio (d = impression diameter, D = ball diameter) for a spherical indenter is 0.375. If tangents are drawn to the ball at the impression edges for d / D = 0.375, they meet below the center of the impression at an angle of 136 degrees, the angle chosen for the Vickers indenter.

Diamond allows the Vickers test to evaluate any material and, furthermore, has the very important advantage of placing the hardness of all materials on one continuous scale. This is a major disadvantage of Rockwell type tests, for which 15 standard and 15 superficial scales were developed. Not one of these scales can cover the full hardness range. The HRA scale covers the broadest hardness range, but this scale is not commonly used.

In the Vickers test, the load is applied smoothly, without impact, and held in place for 10 or 15 seconds. The physical quality of the indenter and the accuracy of the applied load (defined in E 384) must be controlled to get the correct results. After the load is removed, the two impression diagonals are measured, usually with a filar micrometer, to the nearest 0.1 µm, and then averaged. The Vickers hardness (HV) is calculated by:

where the load L is in grams-force and the average diagonal d is in µm (although the hardness number units are expressed in units of kgf / mm² rather than the equivalent gf / µm²).

The original Vickers testers were developed for test loads of 1 to 120 kgf, which produce rather large indents. Recognizing the need for lower test loads, the National Physical Laboratory (U.K.) experimented with lower test loads in 1932. The first low-load Vickers tester was described by Lips and Sack in 1936.

Because the shape of the Vickers indentation is geometrically similar at all test loads, the HV value is constant, within statistical precision, over a very wide test load range, as long as the test specimen is reasonably homogeneous.

However, studies of microindentation hardness test results conducted over the past several years on a wide range of loads have shown that results are not constant at very low loads. This problem, called the "indentation size effect," or ISE, has been attributed to fundamental characteristics of the material. In fact, the same effect is observed at the low load test range of bulk Vickers testers. Furthermore, an ASTM inter-laboratory "round robin" of indents made at one laboratory but measured by twelve different people, reported all three possible ISE responses for the same set of indents!

Since the 1960s, the standard symbol for Vickers hardness per ASTM E 92 and E 384, has been HV. This nomenclature is preferred to the older, obsolete symbols DPN or VPN. The hardness is expressed in a standard format. For example, if a 300 gf load reveals a hardness of 375 HV, the hardness is expressed as 375 HV₃₀₀. Note that ASTM recommends a "soft" metric approach in this case, because rigorous application of the SI system would result in hardness units expressed not in the standard, understandable kgf / mm² values, but in GPa units, which are entirely meaningless to engineers and technicians.

	In the Vickers test, it is assumed that recovery is not elastic after the load is removed. However, in reality recovery is elastic, and sometimes its influence is quite pronounced. Generally, the impression (Fig. 2) appears to be square, and the two diagonals have similar lengths. As with the Brinell test, the Vickers hardness number is calculated based on the surface area of the indent rather than the projected area. However, if the impression shape is distorted by elastic recovery, a very common result in anisotropic materials (Fig. 3), should the hardness be based on the average of the two diagonals? It is possible to calculate the Vickers hardness based on the projected area of the impression, which can be measured by image analysis. Although rigorous studies of this problem are seldom found in the literature, it appears that the diagonal measurement is the preferred approach even for distorted indents.
Fig. 2 - Example of Properly formed indents with excellent image contrast (400X)
Fig. 3 - Example of a distorted Vickers indent in an austenitic stainless steel specimen (400X)

The Knoop test As an alternative to the Vickers test, particularly for very thin layers, Fredrick Knoop and his associates at the former National Bureau of Standards (now NIST) developed a low-load test with a rhombohedral-shaped diamond indenter, Fig. 4. The long diagonal is seven times (7.114 actually) as long as the short diagonal. With this indenter shape, elastic recovery can be held to a minimum. Some investigators claim no elastic recovery with the Knoop indent, but this cannot be true, because measurements of the ratio of  long-to-short diagonal often reveal results substantially different than the ideal 7.114 value.

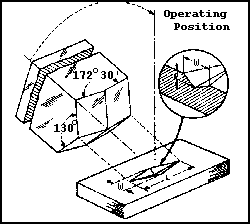Fig. 4 - Schematic showing the shape of the Knoop indenter and impression.

The Knoop test is conducted in the same manner, and with the same tester, as the Vickers test. However, only the long diagonal is measured, except for the projected area hardness (PAH) test recommended by Blau. This, of course, saves some time. The Knoop hardness is calculated from

where the load L is in gf and the long diagonal d is in µm. Again, the symbol HK was adopt in the early 1960s while other terms, such as HKN or KHN, are obsolete. The Knoop hardnness is expressed in the same manner as the Vickers hardness: 375 HK₃₀₀ means that a 300 gf load produced a Knoop hardness of 375 kgf / mm².

Aside from a minor savings of time, one chief merit of the Knoop test is the ability to test thin layers more easily. For surfaces with varying hardness, such as case hardened parts, Knoop indents can be spaced closer together than Vickers indents. Thus, a single Knoop traverse can define a hardness gradient more simply than a series of two or three parallel Vickers traverses in which each indent is made at different depths. Furthermore, if the hardness varies strongly with the depth, the Vickers indent is distorted by this change; that is, the diagonal parallel to the hardness change is affected by the hardness gradient, while the diagonal perpendicular to the hardness gradient remains unaffected (both halves of this diagonal are of the same approximate length).

The shortcoming of the Knoop indent is that the three-dimensional indent shape changes with test load and, consequently, HK varies with load. In fact, HK values may be reliably converted to other test scales only for HK values produced at the standard load, generally 500 gf, that was used to develop the correlations. However, at high loads the variation is not substantial. Note that all hardness scale conversions are based on empirical data; consequently, conversions are not precise but are estimates.

Accuracy, precision, and bias
Many factors (see Table) can influence the quality of microindentation test results.

In the early days of low-load (<100 gf) hardness testing, it was quickly recognized that improper specimen preparation can influence hardness test results. Most texts state that improper preparation yields higher test results because the surface contains excessive preparation-induced deformation. While this is certainly true, improper preparation may also create excessive heat, which reduces the hardness and strength of many metals and alloys. Either problem may be encountered due to faulty preparation.

For many years, it was considered necessary to electrolytically polish specimens so that the preparation-induced damage could be removed, thus permitting bias-free low-load testing. However, the science behind mechanical specimen preparation, chiefly due to the work of Len Samuels, has led to development of excellent mechanical specimen preparation procedures, and electropolishing is no longer required.

In addition, several operational factors must be controlled for optimum test results. First, it is good practice to inspect the indenter periodically for damage; for example, cracking or chipping of the diamond. If you have metrology equipment, you can measure the face angles and the sharpness of the tip. Specifications for Vickers  and Knoop indenter geometries are given in E 384.

A prime source of error is the alignment of specimen surface relative to the indenter. The indenter itself must be properly aligned perpendicular (±1°) to the stage plate. Next, the surface must be perpendicular to the indenter. Most testers provide holders that align the polished face perpendicular to the indenter (parallel to the stage).

If a specimen is simply placed on the stage surface, its back surface must be parallel to its polished surface. Tilting the surface more than one degree from perpendicular results in nonsymmetrical impressions, and can produce lateral movement between specimen and indenter.

However, in most cases, indenting procedures are not the major source of error. For example, the writer has encountered units that were not applying the correct load, as shown in Fig. 5. Tester A produced nearly constant results over the full load range, while tester B produced the correct results only at 1000 gf. As the applied load decreased, the hardness decreased to less than 25% of the correct value! Apparently, the load being applied, for loads under 1000gf, must have been substantially greater than specified. After such an evaluation, it is easy to decide which tester to purchase!

As this experience shows, it is important to regularly check the performance of your tester with a certified test block. The safest choice is a test block manufactured for microindentation testing and certified for the test (Vickers or Knoop) as well as the specified load. Strictly speaking, a block certified for Vickers testing at 300 or 500 gf (commonly chosen loads) should yield essentially the same hardness with loads from about 50 to 1000 gf. That is, if you take the average of about five indents and compare the average at your load to the average at the calibrated load (knowing the standard deviation of the test results), statistical tests can tell you (at any desired confidence level) if the difference between the mean values of the tests at the two loads is statistically significant or not.

When considering a new tester, it is prudent to perform a series of indents (five is adequate) at each test load available (as shown in Fig. 5). Then, plot the mean and 95% confidence limits (not shown in Fig. 5) of each test as a function of load. Because of the method of defining HV and HK, which involves dividing by d2, measurement errors become more critical as d gets smaller; that is, as L decreases and the material's hardness increases. Therefore, departure from a constant hardness for the Vickers or Knoop tests as a function of load becomes a greater problem as the hardness increases. For the Knoop test, HK increases as L decreases because the indent geometry changes with indent depth and width. But the change in HK varies with the test load -- at a higher hardness, the change is greater as L decreases.

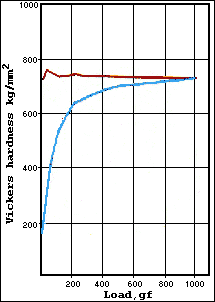Fig. 5 - Load vs. Vickers hardness test results for two testers using a quenched and tempered 440C martensitic stainless steel specimen. Tester A is red, tester B is blue.

The greatest source of error is measuring the indent, as documented in an ASTM inter-laboratory test. Place the indent in the center of the measuring field, because lens image quality is best in the center. The light source should provide adequate, even illumination to provide maximum contrast and resolution. The accuracy of the filar micrometer, or other measuring device, should be verified by a stage micrometer.

Specimen preparation quality becomes more important as the load decreases, and it must be at an acceptable level. Specimen thickness must be at least 2.5 times the Vickers diagonal length. Because the Knoop indent is shallower than the Vickers at the same load, somewhat thinner specimens can be tested.

Spacing of indents is important because indenting produces plastic deformation and a strain field around the indent. If the spacing is too small, the new indent will be affected by the strain field around the last indent. ASTM recommends a minimum spacing (center to edge of adjacent indent) of 2.5 times the Vickers diagonal.

For the Knoop test, in which the long diagonals are parallel, the spacing is 2.5 times the short diagonal. The minimum recommended spacing between the edge of the specimen and the center of the indent should be 2.5 times. Again, Knoop indents can be placed closer to the surface than Vickers indents.

For more information: George F. Vander Voort is director of research & technology, and Gabriel M. Lucas is a materials engineer at Buehler Ltd., 41 Waukegan Road, Lake Bluff, IL 60044; tel: 847 / 295-4590; fax: 847 / 295-7942; e-mail: gfvandervoort@compuserve.com; Web site: www.buehlerltd.com.